大概几个月前,神经网络、人工智能等概念在我心里仍高不可攀,直到自己亲身上手之后,才发现搭建神经网络并不像自己想象的那么难。很幸运,我开始学习神经网络的时候Tensorflow2.0已经发布了。
Tensorflow2中内置了Keras库,Keras是一个由Python编写的开源人工神经网络库,可以作为Tensorflow、Microsoft-
CNTK和Theano的高阶应用程序接口,进行深度学习模型的设计、调试、评估、应用和可视化。用Tensorflow2中自带的Keras库,会使得搭建神经网络变得非常简单友好。
学习神经网络需要的前置知识有:
numpy(必需);pandas;matplotlib
搭建过程
接下来,介绍用tensorflow.keras搭建基本神经网络模型的过程:
1. 引入必需的库
1
2
| import tensorflow as tf
import numpy as np
|
2. 引入数据集
这里的mnist数据集是tf.keras自带的手写数据集,里面存有60000张28x28尺寸的黑白手写数字
1
2
3
4
|
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test= x_train / 255.0, x_test / 255.0
|
3. 搭建神经网络层
Flatten层用于将二维数组展开,相当于把图片按照每一行铺平;Dense层就是所谓的全连接神经网络层,第一个参数是神经元的数量,第二个参数是激活函数的类型;relu函数是一种线性整流函数,在神经网络中有广泛的使用;softmax是一种逻辑回归函数,常用于多分类问题,可以使输出值符合概率分布,神经元数量为10,代表会输出10个元素的列表,列表的每个元素相加为1,列表中的每个元素正好符合对应数字的概率(数字有0~9十种)
1
2
3
4
5
6
7
| model = tf.keras.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')])
|
这就是softmax函数,可以看到对于任意x,其对应的y值都在-1~1之间,从而实现数据的归一化。

4. 编译神经网络模型
- 第一个参数指定优化器为
adam,adam结合了自适应梯度算法和均方根传播,是一个非常强大的优化器
- 指定损失函数的计算方法为交叉熵,
from_logits=False表示数据不是原始输出,即数据满足概率分布,因为我们采用softmax作为输出层,因此结果是概率分布的
- 指定准确率计算方法为多分类准确率
1
2
3
4
5
6
|
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
|
5. 训练模型
- 第一个参数表示输入的训练集,第二个参数表示训练集本身对应的结果,神经网络可以通过判断自己得出的结果与原来给定的结果是否相同,来不断优化自己的判断;
batch_size表示每次喂入的数据量,mnist数据集中有60000张图片,显然不能一次喂入;epochs表示训练次数;validation_data表示验证用的数据集,验证集并不参与训练,因此用验证集判断模型的准确率是客观有效的;validation_freq表示验证频率,即多少次训练会做一次验证
1
2
| model.fit(x_train, y_train, batch_size=32, epochs=10,
validation_data=(x_test, y_test), validation_freq=1)
|
到这里,一个完整的简单神经网络就搭建完成了,我们可以欣赏一下输出结果,这里只截取了第1次和最后2次训练的部分内容,以节省篇幅。
可以看到,每次喂入数据之后,都显示出了训练集的loss误差和accuracy准确率,而当每次训练完成时会进行一次验证,计算出验证集的误差和准确率。
我们还发现一个现象,第一次训练时,每次喂入数据都使得loss误差快速下降,正确率上升,而到最后几次训练时,由于准确率已经很高,想要继续优化模型变得困难,准确率便上下波动,不再持续上升:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| Epoch 1/10
1/1875 [..............................] - ETA: 0s - loss: 2.4223 - sparse_categorical_accuracy: 0.0625
277/1875 [===>..........................] - ETA: 2s - loss: 0.5614 - sparse_categorical_accuracy: 0.8380
567/1875 [========>.....................] - ETA: 1s - loss: 0.4153 - sparse_categorical_accuracy: 0.8792
814/1875 [============>.................] - ETA: 1s - loss: 0.3604 - sparse_categorical_accuracy: 0.8956
1107/1875 [================>.............] - ETA: 1s - loss: 0.3189 - sparse_categorical_accuracy: 0.9070
1367/1875 [====================>.........] - ETA: 0s - loss: 0.2925 - sparse_categorical_accuracy: 0.9150
1592/1875 [========================>.....] - ETA: 0s - loss: 0.2761 - sparse_categorical_accuracy: 0.9197
1875/1875 [==============================] - 3s 2ms/step - loss: 0.2577 - sparse_categorical_accuracy: 0.9250 - val_loss: 0.1379 - val_sparse_categorical_accuracy: 0.9584
Epoch 9/10
1/1875 [..............................] - ETA: 0s - loss: 0.0043 - sparse_categorical_accuracy: 1.0000
347/1875 [====>.........................] - ETA: 2s - loss: 0.0174 - sparse_categorical_accuracy: 0.9986
634/1875 [=========>....................] - ETA: 1s - loss: 0.0173 - sparse_categorical_accuracy: 0.9965
922/1875 [=============>................] - ETA: 1s - loss: 0.0176 - sparse_categorical_accuracy: 0.9945
959/1875 [==============>...............] - ETA: 1s - loss: 0.0177 - sparse_categorical_accuracy: 0.9944
1286/1875 [===================>..........] - ETA: 0s - loss: 0.0182 - sparse_categorical_accuracy: 0.9943
1501/1875 [=======================>......] - ETA: 0s - loss: 0.0187 - sparse_categorical_accuracy: 0.9943
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0193 - sparse_categorical_accuracy: 0.9942 - val_loss: 0.0879 - val_sparse_categorical_accuracy: 0.9763
Epoch 10/10
1/1875 [..............................] - ETA: 0s - loss: 0.0164 - sparse_categorical_accuracy: 0.9995
322/1875 [====>.........................] - ETA: 2s - loss: 0.0131 - sparse_categorical_accuracy: 0.9986
610/1875 [========>.....................] - ETA: 1s - loss: 0.0138 - sparse_categorical_accuracy: 0.9976
999/1875 [==============>...............] - ETA: 1s - loss: 0.0146 - sparse_categorical_accuracy: 0.9970
1248/1875 [==================>...........] - ETA: 0s - loss: 0.0147 - sparse_categorical_accuracy: 0.9965
1285/1875 [===================>..........] - ETA: 0s - loss: 0.0148 - sparse_categorical_accuracy: 0.9959
1536/1875 [=======================>......] - ETA: 0s - loss: 0.0153 - sparse_categorical_accuracy: 0.9954
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0157 - sparse_categorical_accuracy: 0.9952 - val_loss: 0.0804 - val_sparse_categorical_accuracy: 0.9789
|
到这里,我们的模型就输入完成了,只需要提供一个输入图片的函数,便可以完成看图识别数字的任务:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| import PIL.Image
def judge_image(path):
"""输入图片的路径,判断图片中的数字是什么"""
img = Image.open(path)
img = img.resize((28, 28))
img_array = np.array(img.convert('L'))
for row in range(28):
for col in range(28):
if img_array[row][col] < 75:
img_array[row][col] = 255
else:
img_array[row][col] = 0
img_array = img_array / 255.0
x_predict = img_array[tf.newaxis]
result = model.predict(x_predict)
predict = tf.argmax(result, axis=1)
tf.print(predict)
|
这样,完整的代码就完成了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| import tensorflow as tf
import numpy as np
import PIL
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test= x_train / 255.0, x_test / 255.0
model = tf.keras.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')])
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train, y_train, batch_size=32, epochs=10,
validation_data=(x_test, y_test), validation_freq=1)
def judge_image(path):
img = PIL.Image.open(path)
img = img.resize((28, 28))
img_array = np.array(img.convert('L'))
for row in range(28):
for col in range(28):
if img_array[row][col] < 75:
img_array[row][col] = 255
else:
img_array[row][col] = 0
img_array = img_array / 255
x_predict = img_array[tf.newaxis]
result = model.predict(x_predict)
predict = tf.argmax(result, axis=1)
tf.print(predict)
|
效果测试
我们来试一下预测效果,我准备了几张手写数字的图片:
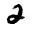 img_2.gif
img_2.gif
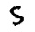 img_5.gif
img_5.gif
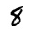 img_8.gif
img_8.gif
1
2
3
4
| for i in 2,5,8:
print("The recognized figure of img_%d.gif: " % i, end='')
judge_image('images/img_%d.gif' % i)
time.sleep(1)
|
输出结果为:
1
2
3
| The recognized figure of img_2.gif: [2]
The recognized figure of img_5.gif: [5]
The recognized figure of img_8.gif: [8]
|
可以看到,每张图片所对应的数字都被识别出来啦!

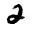 img_2.gif
img_2.gif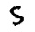 img_5.gif
img_5.gif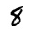 img_8.gif
img_8.gif