我们知道生活中的很多现象,比如身高体重的分布,都满足高斯分布 (正态分布)。而高斯混合模型,则是通过多个高斯分布的叠加,实现对数据集的拟合。
高斯分布
如果学过概率论,我们知道高斯分布的公式如下:
$$
X \sim N(\mu,\sigma^2)
$$
生活中的很多现象,比如身高,都近似一种高斯分布:
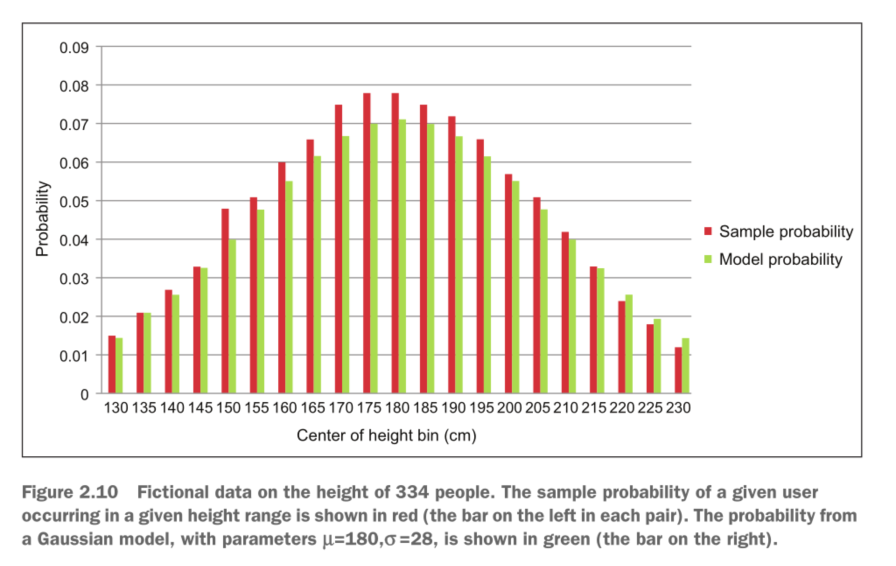
考虑一个问题,如果有一组数据,其中包括男性和女性的身高,比起使用一个高斯分布,使用两个高斯分布拟合的效果是不是更好呢?
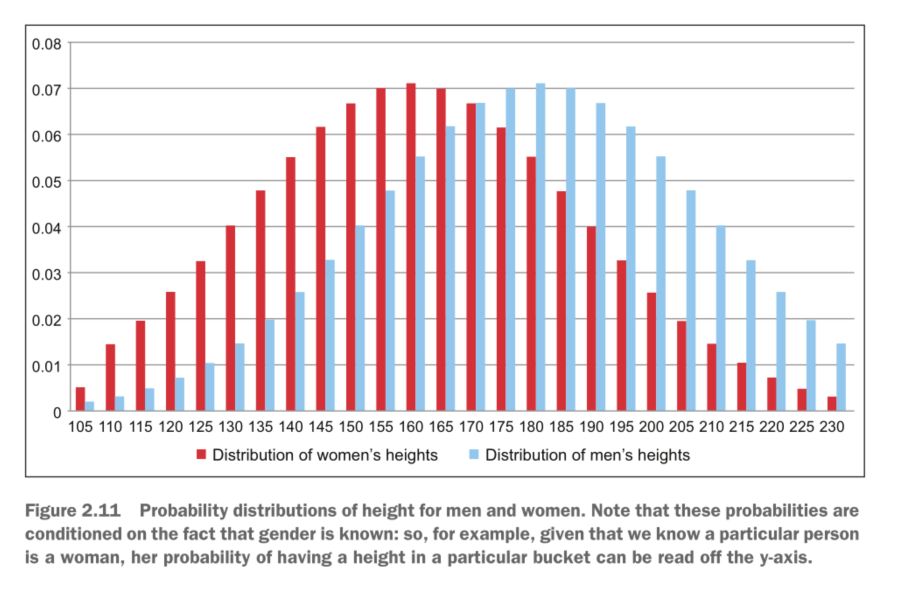
然而,我们只知道数据集,并不知道分布的参数,高斯混合要做的,就是把每个高斯分布的参数求出来。
多元高斯分布
多元高斯分布的公式如下:
$$
p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}
$$
- $\mu$ 是 n 维均值向量
- $\Sigma$ 是 $n\times n$ 的协方差矩阵
高斯混合模型 (GMM)
考虑数据集
| 编号 | 密度 | 含糖率 |
|---|---|---|
| 1 | 0.697 | 0.460 |
| 2 | 0.774 | 0.376 |
| 3 | 0.634 | 0.264 |
| 4 | 0.608 | 0.318 |
| 5 | 0.556 | 0.215 |
| 6 | 0.403 | 0.237 |
| 7 | 0.481 | 0.149 |
| 8 | 0.437 | 0.211 |
| 9 | 0.666 | 0.091 |
| 10 | 0.243 | 0.267 |
初始化
首先考虑将数据集分成几类,比如分 3 类。
接下来就需要初始化 3 个类,也就是三个高斯分布的参数:
初始化三个高斯分布的权重各为 1/3
$$
\alpha_1=\alpha_2=\alpha_3=0.3333
$$
初始化三个高斯分布的协方差矩阵,由于样本集有 2 个维度,故高斯分布也满足二维
$$
\Sigma_1=\Sigma_2=\Sigma_3=\begin{pmatrix}
0.1 & 0 \
0 & 0.1
\end{pmatrix}
$$
随机选择 3 个样本作为 3 个高斯分布的初始参数
$$
\mu_1=x_2=(0.774,0.376)
$$
$$
\mu_2=x_5=(0.556,0.215)
$$
$$
\mu_3=x_8=(0.437,0.211)
$$
求出每个样本对于每个高斯分布的概率密度
$$
p_1(x_1) = \frac{1}{2\pi|\Sigma_1|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_1-\mu_1)^T\Sigma_1^{-1}(x_1-\mu_1)}
$$
其中
$$
|\Sigma_1|=0.01
$$
$$
x_1-\mu_1=\begin{pmatrix}
-0.077 & 0.084
\end{pmatrix}
$$
计算得到
$$
p_1(x_1) = 0.1472
$$
同理
$$
p_2(x_1) = \frac{1}{2\pi|\Sigma_2|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_1-\mu_2)^T\Sigma_1^{-1}(x_1-\mu_2)}
$$
计算得到
$$
p_2(x_1)=0.1053
$$
$$
p_3(x_1) = \frac{1}{2\pi|\Sigma_3|^{\frac{1}{2}}}e^{-\frac{1}{2}(x_1-\mu_3)^T\Sigma_1^{-1}(x_1-\mu_3)}
$$
$$
=0.0822
$$
因此 $x_1$ 属于第 1 类的概率最大,归入第 1 类。
经过对 10 个样本的计算,所有样本都被归类:
第一类:1, 2
第二类:3, 4, 5, 9
第三类:6, 7, 8, 10